At first, I was a bit confused by the need for a combiner function. However, I started thinking of this parallelized fold as I would a divide and conquer algorithm like merge sort. The combiner function in this particular analogy mimics the recursive merging of two partially sorted arrays. The combiner function helps us get to the same single answer the sequential implementation would provide.

Can we categorize the overhead of this with big-O? Is it perhaps O(log n)?

@alrcdilaliaou I assume by overhead, you are referring to the comb operations and not the f function calls. In that case, it looks like the big-O is O(log (n/num batches)) = O(log n). I may have missed this in lecture, but how would the batch size be determined? I bet it is related to the architecture of the processor.

I understand how this is parallel, but in order to perform this do we need to divide the initial a and b into chunks? If we don't divide it up, why are we combining?

When we are calling the fold function, do we need to also specify the combiner function in order for the parallel fold to be implemented (in the case the "a" and "b" is not of the same type).

When parallelizing this, are we parallelizing the non-dependent functions here, such as accumulating the value for both a and b then parallelizing the combos?

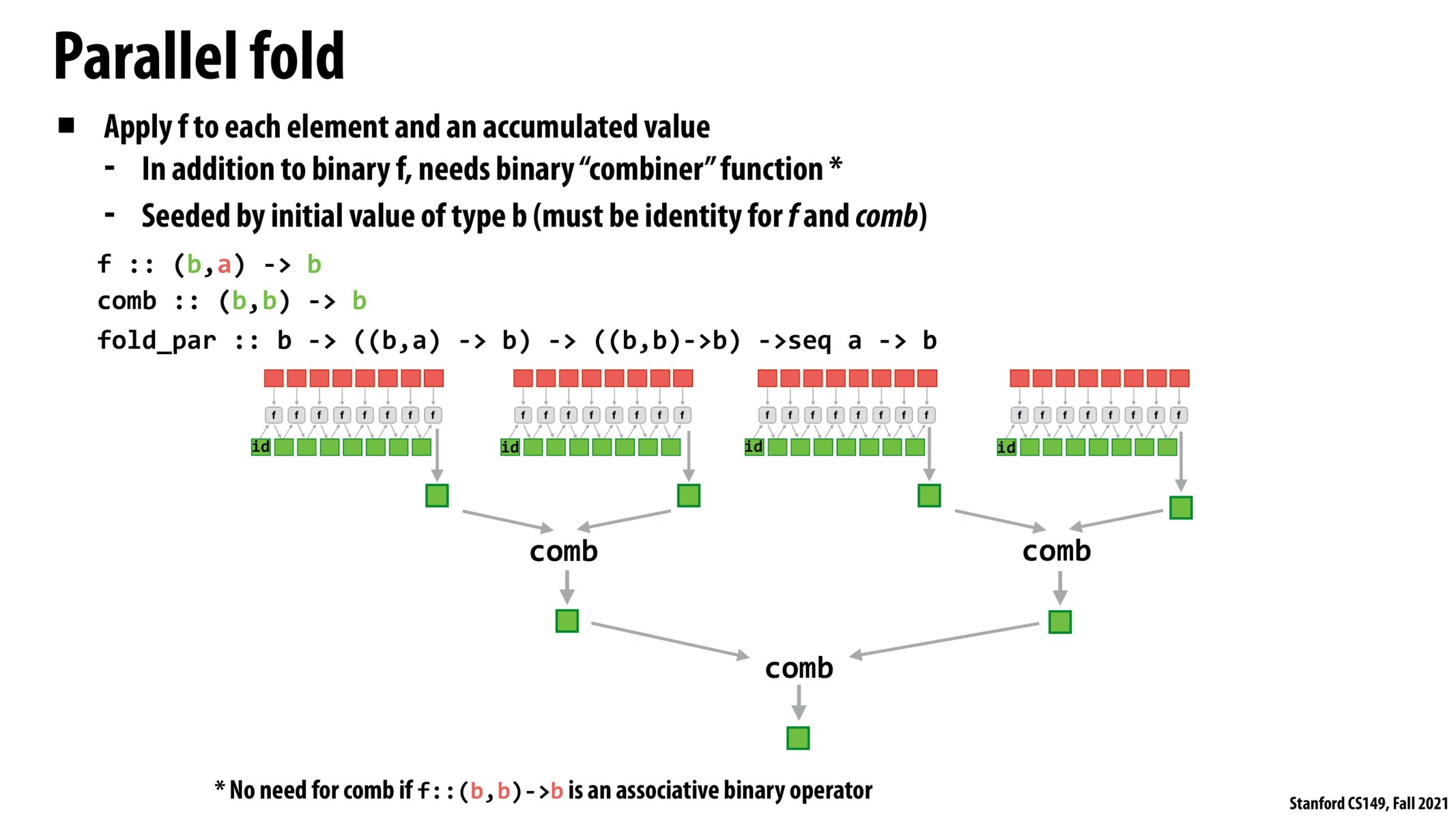
Fold, as it was originally described is not a parallel operator due to the dependency chain across the addition. The way this modification makes it parallelizable by adding a new function - the combiner. Parallel fold takes in f, the combiner, a starting element, and an input sequence, and runs the sequential fold in parallel on chunks. Then the combiner combines the results. As ismael pointed out, this is analogous to recursively merging in a divide and conquer algorithm.