Is this a valid solution to this? if (i == 0) { t = 42.0; } else { t = x[i-1] + 73.0; }

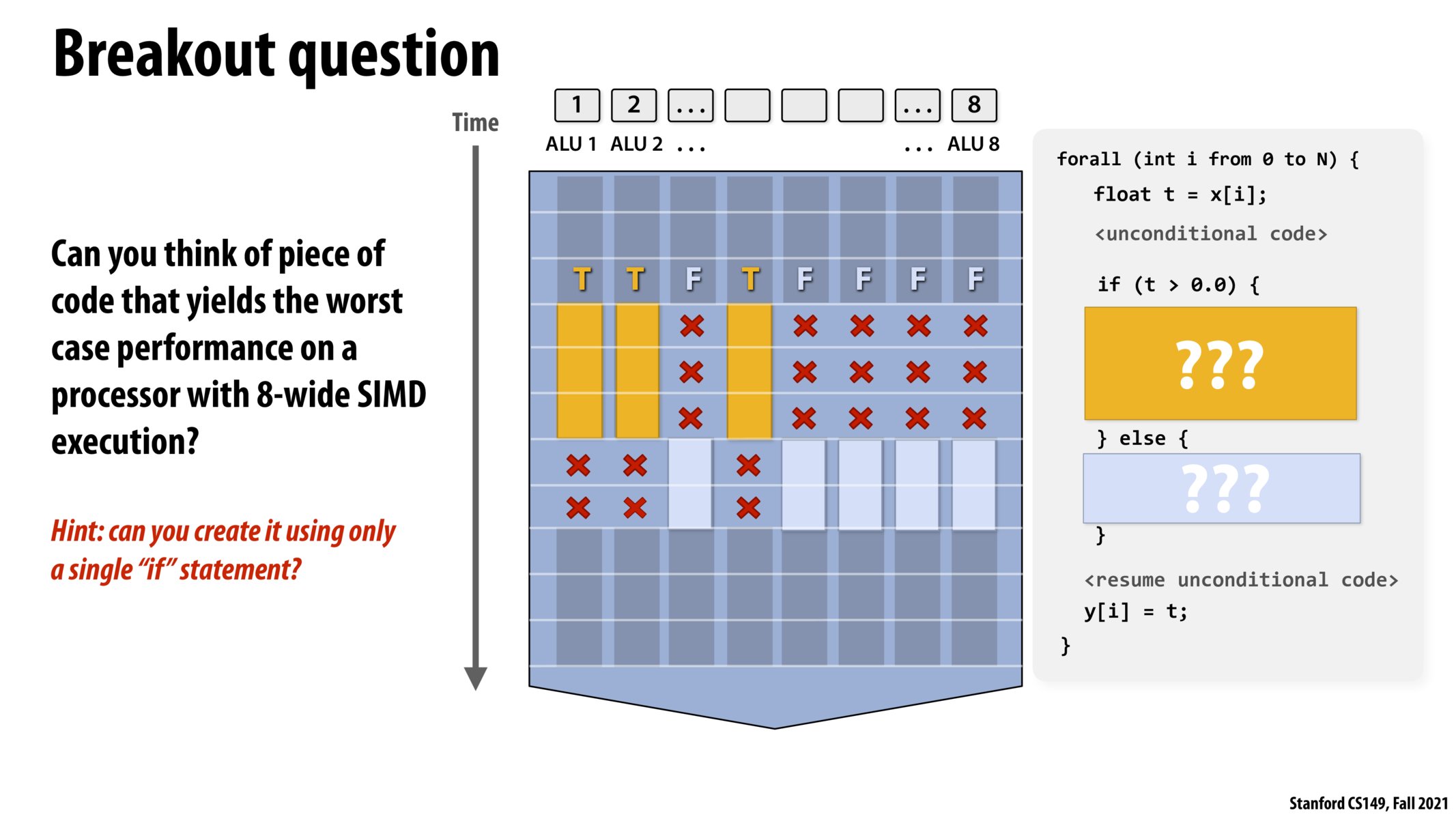
If I understand this one correctly, if there was only 1 T and 7 F (or vice versa), we would be at 50% performance if the time to run each condition is the same. But the worse case performance here can be way lower, which happens if one of the conditions has code that takes much longer to run than the other condition and only one thread is doing useful work for that condition. Please correct me if I'm wrong as I am still a little bit confused about this.

I would do something like this: if( (i%8) == 0) ){ //Do something on just 1 ALU for a while. }

@jasonalouda, I was pretty confused about this too, and I found that plugging in numbers helped a lot to reason why the worst case is 1/8 peak performance. Here are the examples I used:

Example 1: 8 iterations, in which the if branch takes 10 instructions, the else branch takes 10 instructions, and each instruction takes 1 cycle to execute. It takes our 8-lane ALU 10 + 10 = 20 cycles to pre-compute both the if and else branches. If we only take the if branch once out of every 8 iterations, then the number of useful instructions ran is 10 + 710 = 80 (1 if branch and 7 else branches). At peak performance, in the time it takes for our 8-lane ALU to complete execution (20 cycles), we could have ran 820 = 160 useful instructions. 80/160 = 50% of peak performance

Example 2: 8 iterations, in which the if branch takes 1000 instructions, the else branch takes 10 instructions, and each instruction takes 1 cycle to execute. It takes our 8-lane ALU 1000 + 10 = 1010 cycles to pre-compute both the if and else branches. If we only take the if branch once, then the number of useful instructions ran is 1000 + 710 = 1070 (1 if branch and 7 else branches). At peak performance, in the time it takes for our 8-lane ALU to complete execution (1010 cycles), we could have potentially ran 81010 useful instructions. 1070/8080 ~= 1/8 of peak performance (tends to 1/8 as the number of instructions the if branch takes increases relative to the else branch)

Example 3: 8 iterations, in which the if branch takes 10 instructions, NO ELSE BRANCH as Pranil suggested in lecture, and each instruction takes 1 cycle to execute. It takes our 8-lane ALU 10 cycles to pre-compute the if branch. If we only take the if branch once, then the number of useful instructions ran in that time is 10. At peak performance, in the time it takes for our 8-lane ALU to complete execution (10 cycles), we could have potentially ran 8*10 useful instructions. 10/80 = 1/8 of peak performance

Fixed the markdown formatting from the post above.

Example 1: * 8 iterations, in which the if branch takes 10 instructions, the else branch takes 10 instructions, and each instruction takes 1 cycle to execute. * It takes our 8-lane ALU 10 + 10 = 20 cycles to pre-compute both the if and else branches. * If we only take the if branch once out of every 8 iterations, then the number of useful instructions ran is 10 + (7)(10) = 80 (1 if branch and 7 else branches). * At peak performance, in the time it takes for our 8-lane ALU to complete execution (20 cycles), we could have ran (8)(20) = 160 useful instructions. * 80/160 = 50% of peak performance

Example 2: * 8 iterations, in which the if branch takes 1000 instructions, the else branch takes 10 instructions, and each instruction takes 1 cycle to execute. * It takes our 8-lane ALU 1000 + 10 = 1010 cycles to pre-compute both the if and else branches. * If we only take the if branch once, then the number of useful instructions ran is 1000 + (7)(10) = 1070 (1 if branch and 7 else branches). * At peak performance, in the time it takes for our 8-lane ALU to complete execution (1010 cycles), we could have potentially ran (8)(1010) useful instructions. * 1070/8080 ~= 1/8 of peak performance (tends to 1/8 as the number of instructions the if branch takes increases relative to the else branch)

Example 3: * 8 iterations, in which the if branch takes 10 instructions, NO ELSE BRANCH as Pranil suggested in lecture, and each instruction takes 1 cycle to execute. * It takes our 8-lane ALU 10 cycles to pre-compute the if branch. * If we only take the if branch once, then the number of useful instructions ran in that time is 10. * At peak performance, in the time it takes for our 8-lane ALU to complete execution (10 cycles), we could have potentially ran (8)(10) useful instructions. * 10/80 = 1/8 of peak performance

@schaganty provides some very useful concrete examples. The common confusion seems to be about the definition of what "1/8 performance" or "peak performance" actually means, so I'll try to provide another way of thinking about this situation that might help.

@kcoran's example essentially looks like the following, where one in each 8 iterations uses up lots of cycles while the other 7 are trivial:

``` 1 2 3 4 5 6 7 8 T F F F F F F F

O x x x x x x x O x x x x x x x O x x x x x x x O x x x x x x x . . . O x x x x x x x x O O O O O O O ```

Note that the best possible performance of executing this code on one ALU takes around the same amount of time as the best possible performance on 8 ALUs, meaning that we're wasting 7/8 of our potential.

Another way to think about this visually is to look at the area of the rectangle (with 8 columns and as many rows as total cycles) compared to the area filled up by the orange and grey bars in the slide. In our worst-case example, the total area of the bars is around 1/8 of the area of the rectangle.

RIP, was hoping the markdown would work. In any case, the diagram looks like one big orange bar going down the left and seven negligible gray bars at the bottom :)

So "1/8" of full potential just means that the "if" branch takes 7 times as long as the "else" branch?