Can someone explain how the speedup converges to 2 if n approaches infinity? Taking the limit, we would essentially get 2 / (1/p + 1), so I'm not sure how the speedup is 2 unless we assume p is large as well?

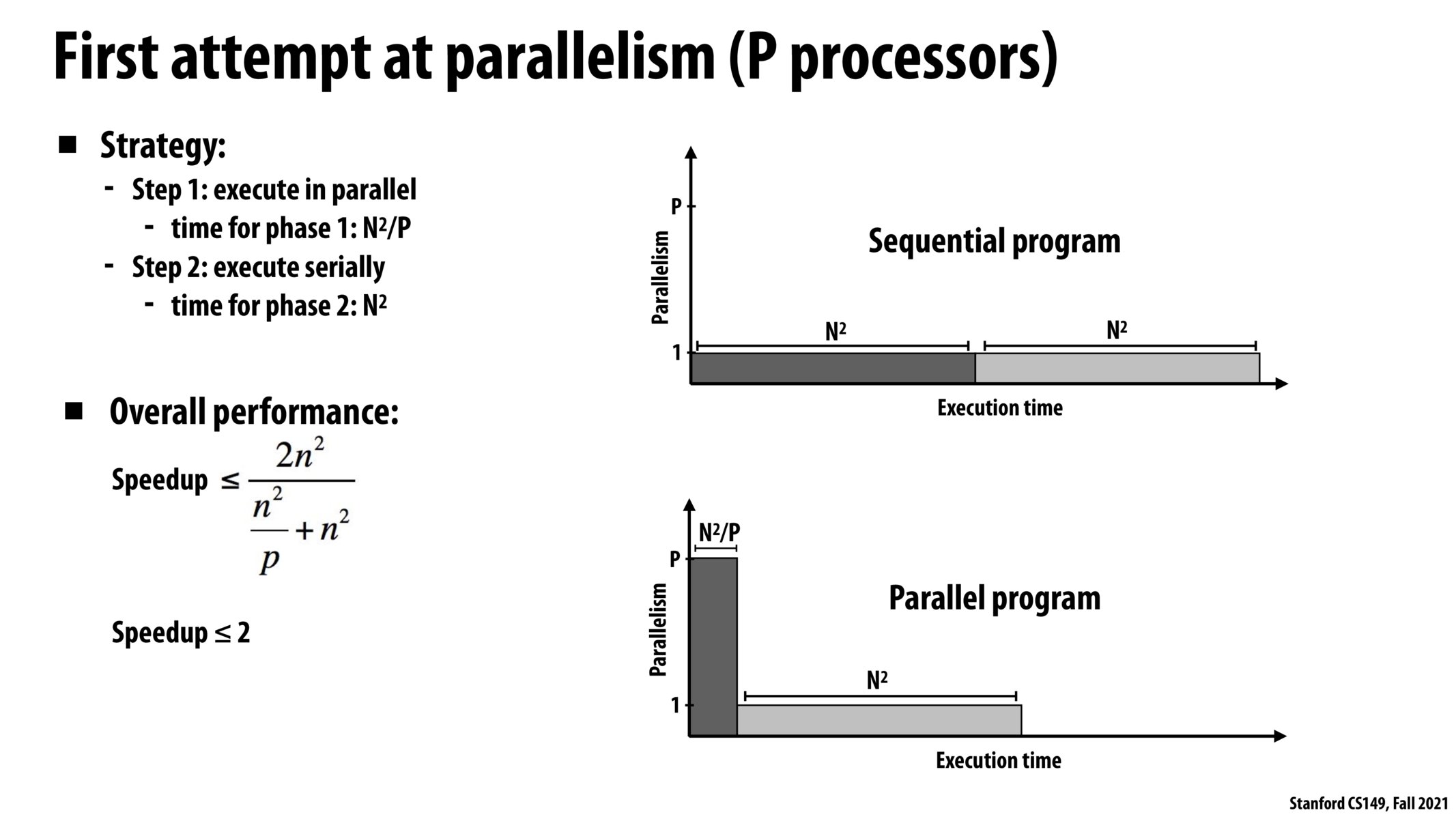
I think in lecture Kayvon mentioned as n->inf , the speedup converges to 2. Should it not be as p->inf, the speedup converges to 2, as speedup = 2/(1/p + 1)?

I'm confused about the speedup <=2 here as well... Is the 2 here just a looser bound for max speedup, since 2/(1/p+1) <= 2?

@gomi I'm pretty sure you're correct, it's simply a looser bound. A few slides back, Kayvon talked about Amdahl's Law, which states that maximum speedup is <= 1/S, where S is a fraction of the code that is inherently sequential. In this case, we are saying that the second half of the code is inherently sequential, so S=1/2 and therefore maximum speedup is <= 1/(1/2) = 2. I guess it's useful to have these quick-to-compute lower bounds in practice for quick calculations/prototyping?

@derrick I think that in lecture, Kayvon actually said that this speedup happens as p approaches infinity, rather than n. This would make the math make sense, and we also notice that this seems like a more sensible question to ask when we're trying to measure the parallelizability of a program.

However, I would also assume that in real cases, there would be some optimal p, not p->inf that maximizes speedup due to the increased overhead of breaking down the problem into too many pieces.