I'm struggling to understand how this equation is related to the inequality on the previous slide. Are we supposed to be able to convert between the two? Additionally, what is "fraction of total work that is inherently sequential" defined as (perhaps an example would help)?

@thepurplecow I think the inequality on the previous slide was just a specific example with a particular runtime growth. This is the more general case.

I think for your second question, imagine a task that takes 10 seconds serially, but you can break up the first 9 seconds of work across threads. The last 1 second depends on results from the first 9, and it cannot be broken up. Then S=0.1, if that makes sense.

As a follow up, I am wondering how this formula is derived...? Maybe I miss something, but I cannot see the intuition behind this formula.

@student1 here is how I understand it.

Suppose serial execution time is X. We can decompose X as X = (1-s)X + sX. In other words, the execution time X can be split up into a parallelizable ((1-s)X) and sequential portion (sX).

If we have P processors, then we see that the parallel portion of our program can be cut to a runtime of at best (1-s)X / P. So our new runtime is X' = (1-s)X / P + s*X. We now get work done in the following fraction of time:

X'/X = ((1-s)X/P + s*X)/X = (1-s)/P + s

Our speedup, which is X / X' (reciprocal of the above), is then 1 / (s + (1-s)/P)

@probreather101, that is a great explanation of Amdahl's law! Intuitive and concise---I didn't quite get it before, but now I do. Excellent contribution.

I think this formula provides the intuition that the goal of a parallel programmer should focus on parallelizing the longest serial part of the program execution as this is the bottleneck in achieving high speedup.

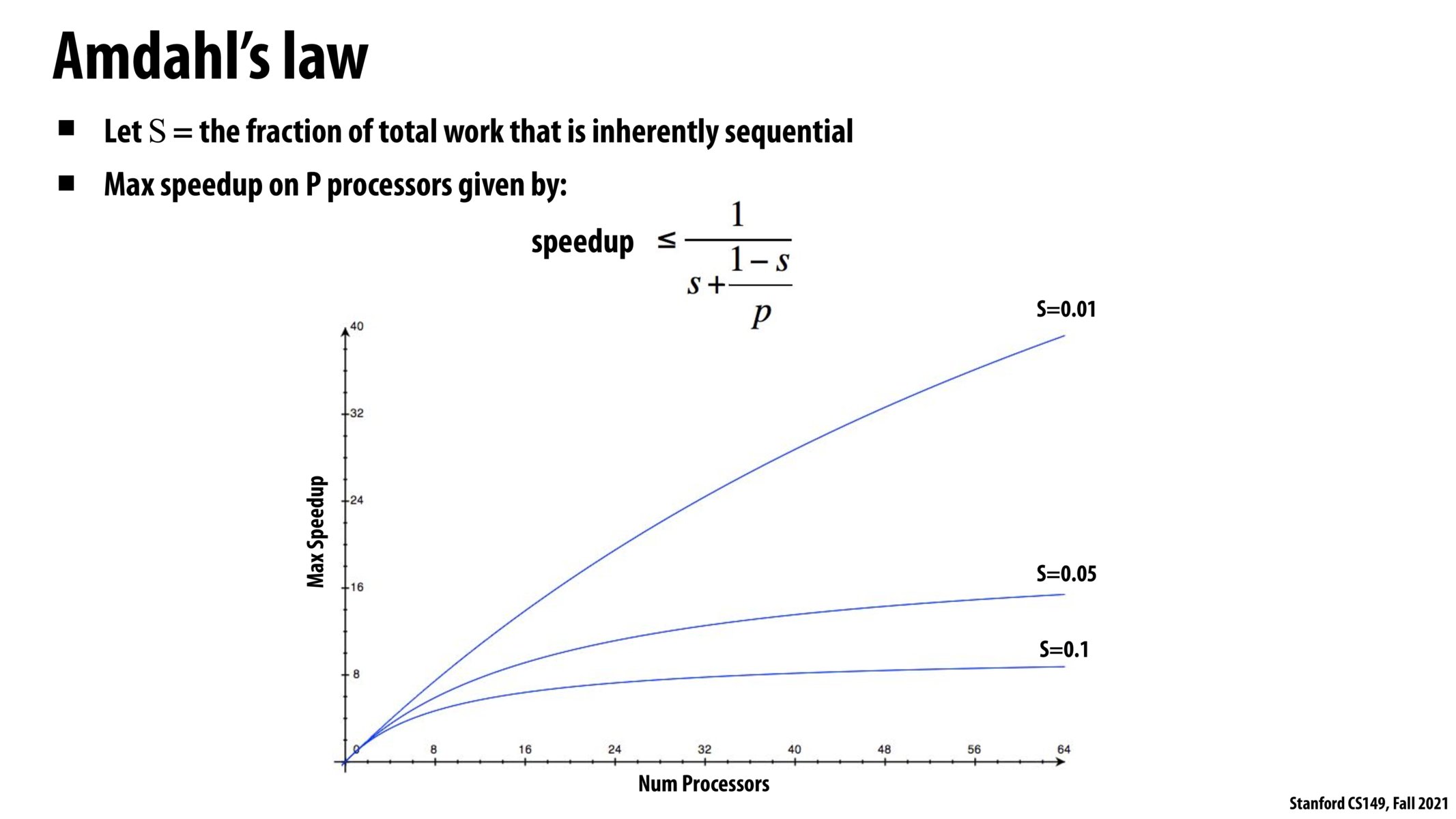
It's super counter intuitive that going from 32 processors to 64 processors gives no speedup for a task thats only 10% serial!

@ayushaga I agree that's how I saw it. The way I thought of this formula is that we know for a fully parallelizable program the expected speedup from using P processors is P however we obviously know that if the program isn't fully parallelizable then we'll have a component/fraction of the program that will get speedup by P (let's call it S) and a sequential component/fraction that will remain the same (1-S) so the new runtime T (as a fraction of the old runtime) is the sum of both so T = S/P + (1-S) for example if P=2, S=0.8 then T = 0.4 + 0.2 = 0.6 so the program would run at 0.6 time compared to the old time of 1 and that's a speed up of 1.6x which is slower than the 2x we'd get since 20% of our program was sequential and if we plug our parameters to Amdahl's law to verify our answer we get (1/(0.2 + (1-0.2)/2)) = 1.6x as well.