One question raised in lecture was whether the image is flipped horizontally or vertically from real life. The answer is both! The tree diagram happens to illustrate the projection on the vertical axis, showing that the top of the tree projects to the bottom of the image. But a similar diagram can be drawn to illustrate the projection on the horizontal axis. The final result is an image that is mirrored in both axes.

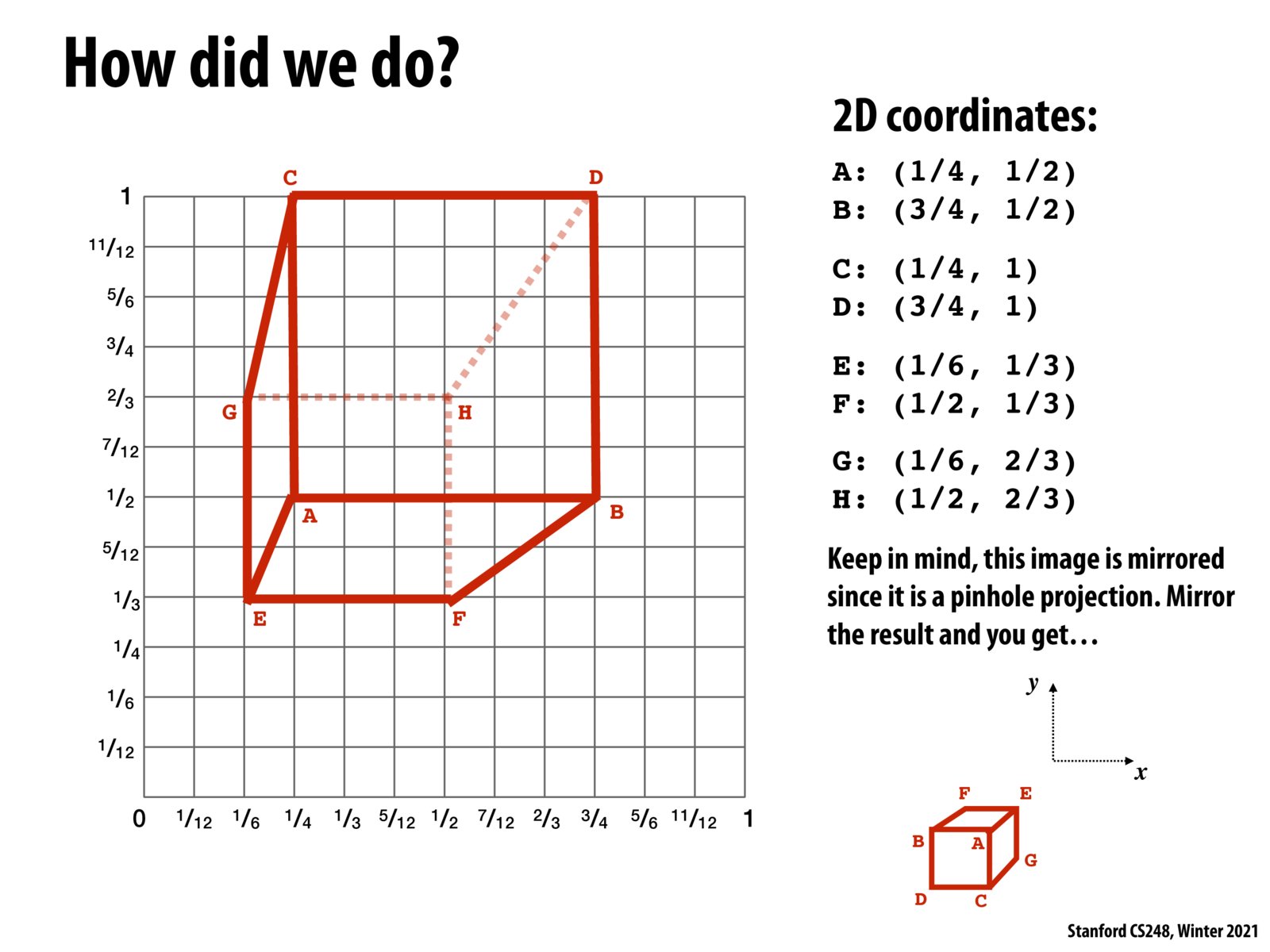
Perhaps another way to explain the mirrored image is due to the sign of the z coordinate of the cube after camera is translated. I think z in this case has minus sign for all vertices. Because u = x / z and v = y / z, u and v will go in separate directions as x and y.

I know this was briefly mentioned in the lecture after a question was asked about camera angle - using this approach, is the camera looking at the origin or straight down? Is there a difference between the two besides translation of the cube?

I think the camera is looking straight down. I don't think the top and bottom surfaces of the cube would be perfectly square otherwise. If the camera was tilted, the opposite edges on these surfaces would no longer be parallel.

There is a proof in CS231A that parallel lines remain parallel after translation and rotation projects. The proof assumes two points on two parallel lines, uses the property of cross product, and expands to show the property still holds after the projections. Why does that not hold in this case?