One question: Is this algorithm volume preserving? It looks like the volume is shrinking when the surface gets smoother.

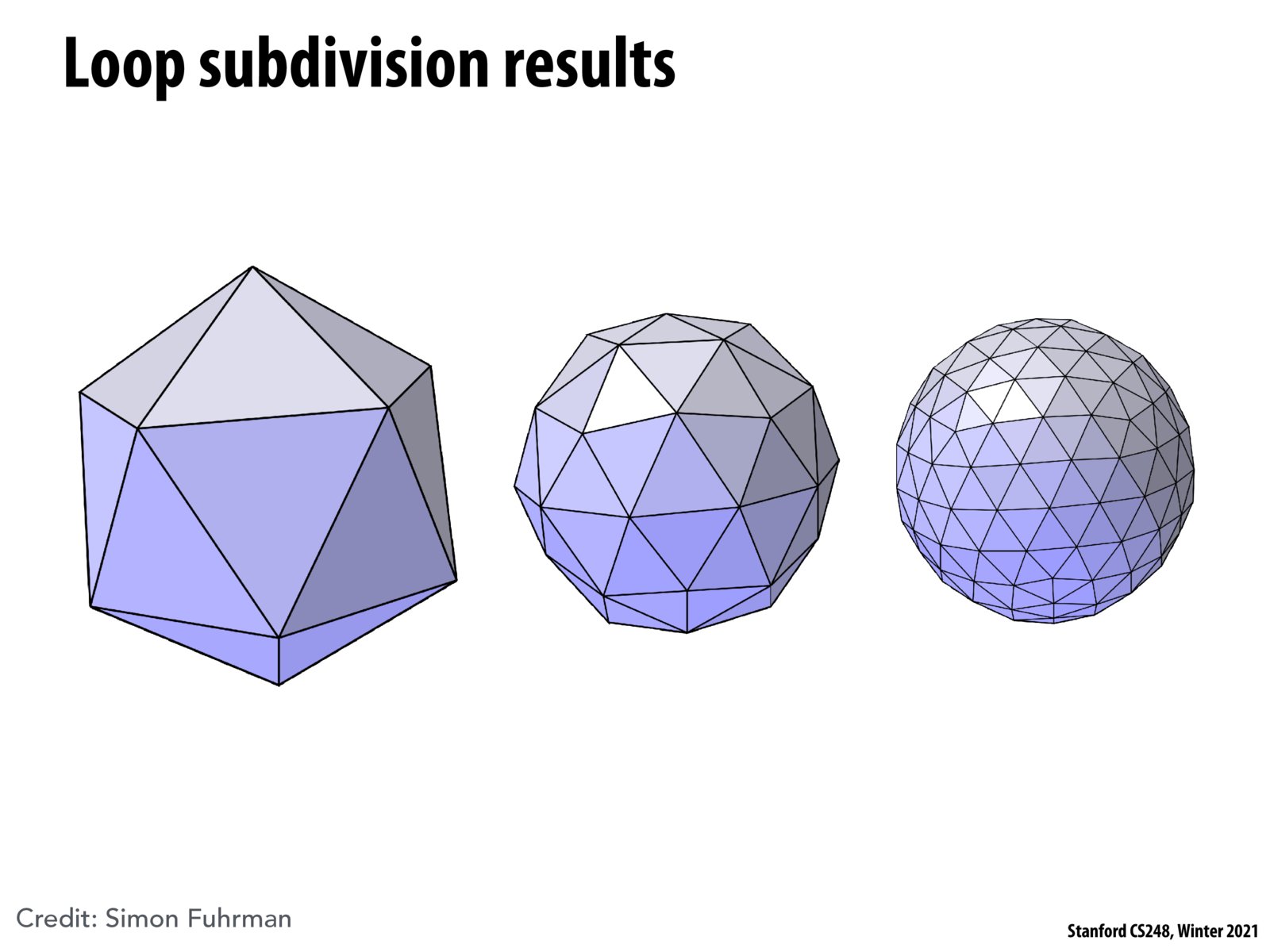
I would think that if the surface area is preserved then the volume is not preserved? Since as the surface gets smoother it becomes closer and closer to a sphere, which I think is the way to maximize volume given a fixed surface area.

How is the surface area preserved?

I don't think either the volume or the surface area is preserved? I think the main goal of the algorithm is to smooth the shape without caring about volume or surface area. You may imagine a pyramid whose height is very large compared to its base surface length. After several iterations of the algorithm, the resulted shape should be much smoother and smaller in size. Its height-length ratio should lower by a lot and both its surface area and volume will also decrease. I believe that such shrinkage would happen for non-smooth objects especially.

While subdividing with triangles might be the best choice in this case to reach a spherical body, it is not always the case. Take for example trying to subdivide a cube into a more spherical form. It would be easier to subdivide the cube by square s rather than triangles to preserve curvature. Like most things we've learned in this course, each approach has its pros and cons and preferred use cases.