It seems that this matrix is only trying to convert the 3D coordinates by normalizing z = 1. I am not sure when to use this matrix.

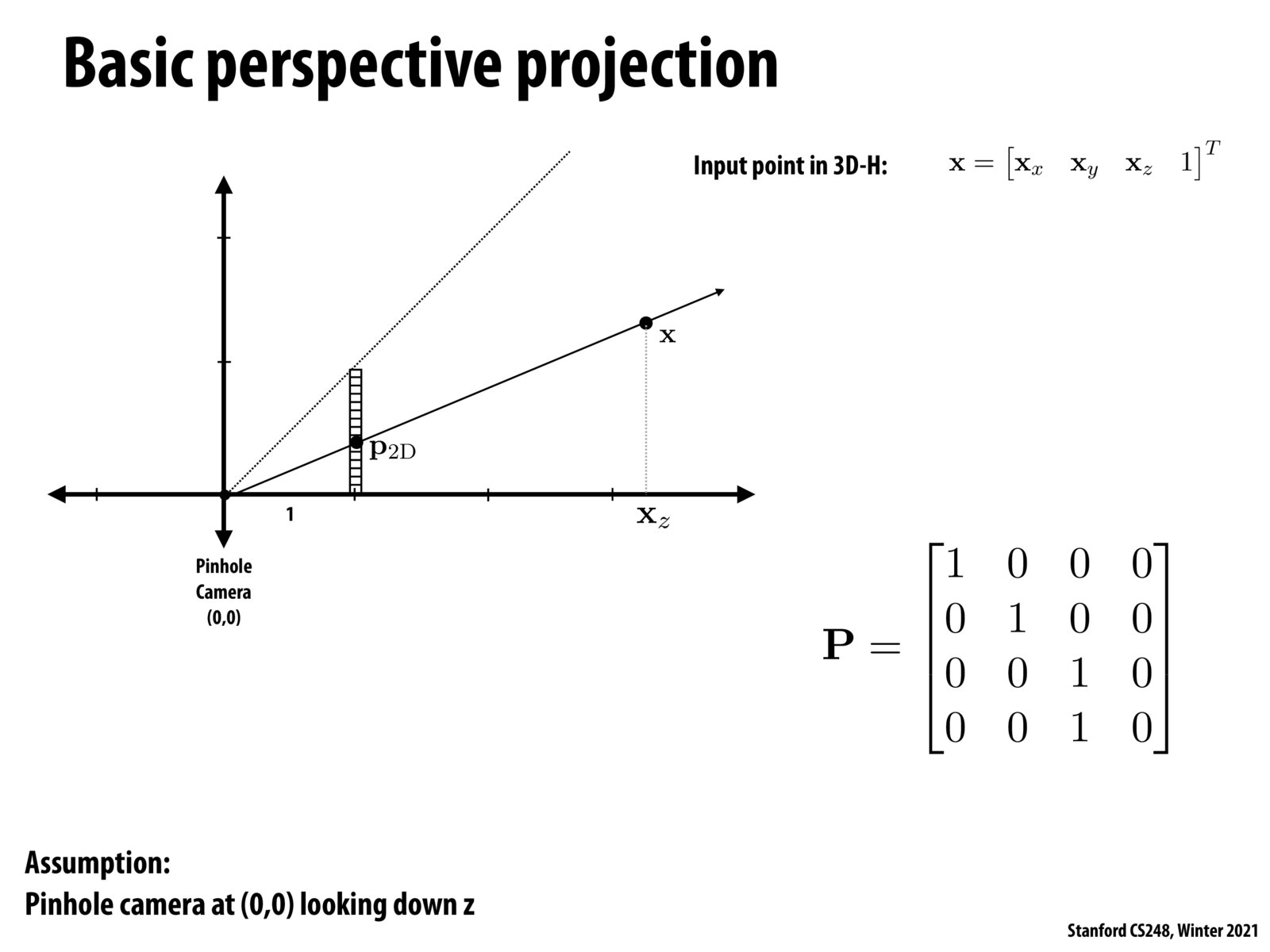
It's a combination of a few ideas. First, we want to be able to compute perspective projections of 3D scenes. Second, we would like our method to be linear (i.e. a single matmul). Constructing the matrix as above would allow us to do just that. With a single matmul (Px = [x_x, x_y, x_z, x_z]), we produce coordinates in 3D-H space which can easily be converted to (u,v) coordinates on the image plane (i.e. p_2D=[u,v]^T=[x_x/x_z x_y/x_z]^T).

The conversion is done by doing the usual homogenous coord -> regular coord operation, bringing our 3D-H coords to 3D space.

[x_x, x_y, x_z, x_z] -> [x_x/x_z, x_y/x_z, 1, 1] -> [x_x/x_z, x_y/x_z, 1].

While we are normalizing z=1, we are also producing the computations necessary for computing the perspective projection seen in Lecture 1, slide 35.

I was struggling a bit to understand the meaning of the perspective matrices, and it was helpful for me to think that perspective gives you a way to represent 3D objects in 2D coordinates, and the way that you would do this is by, for each point (x, y, z) in 3D space that you have, add a corresponding point (x/z, y/z) in 2D space when drawing your image. The transformation f(x, y, z) = (x/z, y/z) would normally not be linear, and the homogeneous coordinates give you a way of making this transformation linear, through this matrix that essentially performs a division by z.