It seems that shear is an area-conserving transformation; is this part of why translation can be done as a shear in homogeneous coordinates?

I think the shearing in +1 dimension of an object results in the projection of the object to the current dimension to be a translation (e.g. a flash light at the origin projecting a 2D image to a 3D plane at z = w. As the flash light changes orientation, or shear in 3D, the projection on the image plane in 2D translates at z = w plane). In addition, the matrix of shearing in 3D is linear, and can be used to translate the 2D points and vector in homogenous coordinate through matrix multiplication.

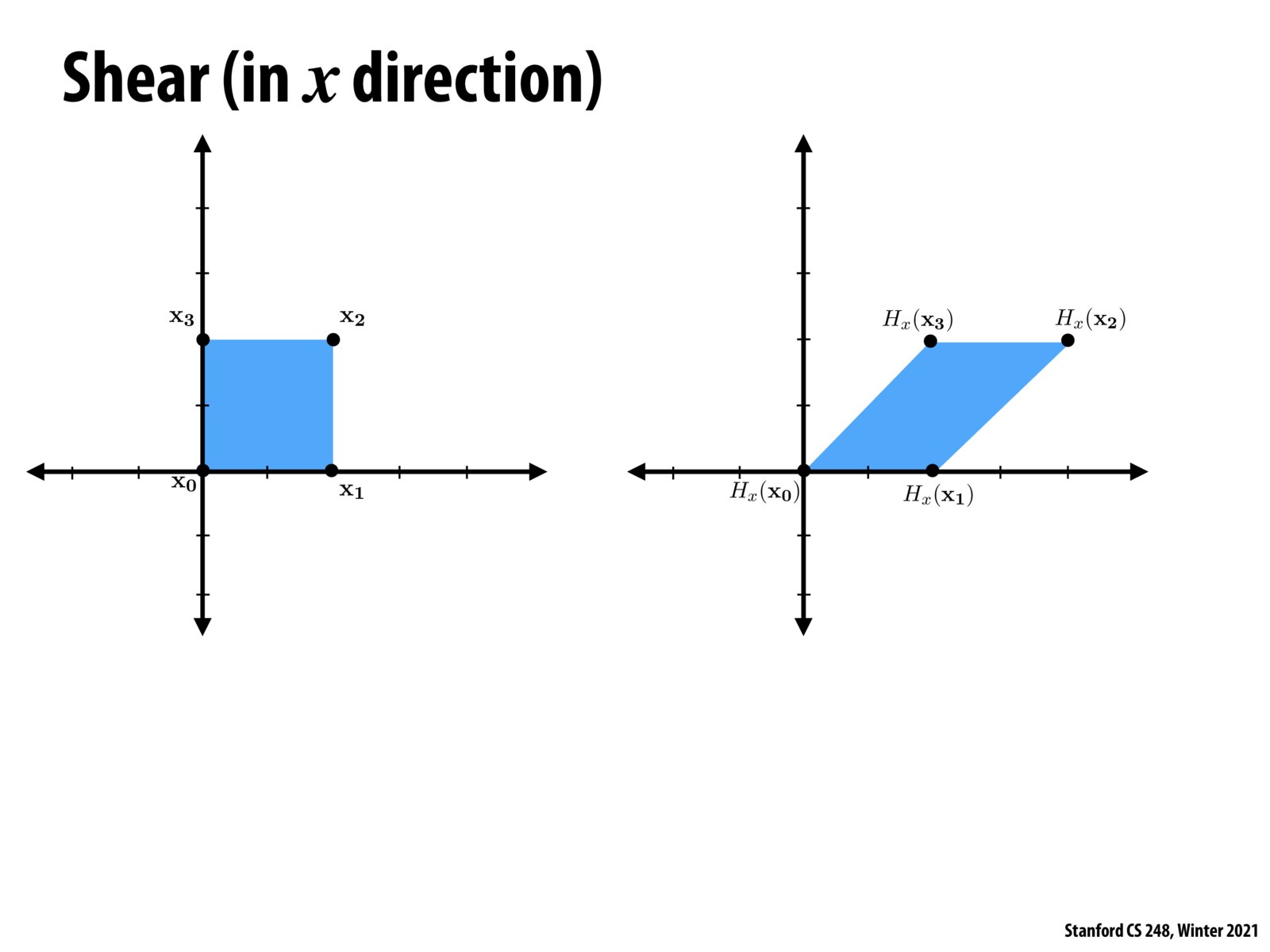
It was mentioned in class that it is easy to show shear is a linear map. For example, consider shear along x: f(x, y) = (x + my, y). First condition for linear transformation: f(x1 + x2, y1 + y2) = (x1 + x2 + my1 + my2, y1 + y2) = (x1 + my1, y1) + (x2 + my2, y2) = f(x1, y1) + f(x2, y2) (first property holds). Second condition: f(ax, ay) = (ax + amy, ay) = a(x + my, y) = f(x, y) (second property holds).