Under what circumstances or practical applications would one want to map this polygon into a nonlinear map as shown? It seems to me kind of strange that anyone would even consider creating a nonlinear map to transform this pentagon into this amorphous blob, but perhaps there are some practical reasons that I'm neglecting where a nonlinear map might be useful?

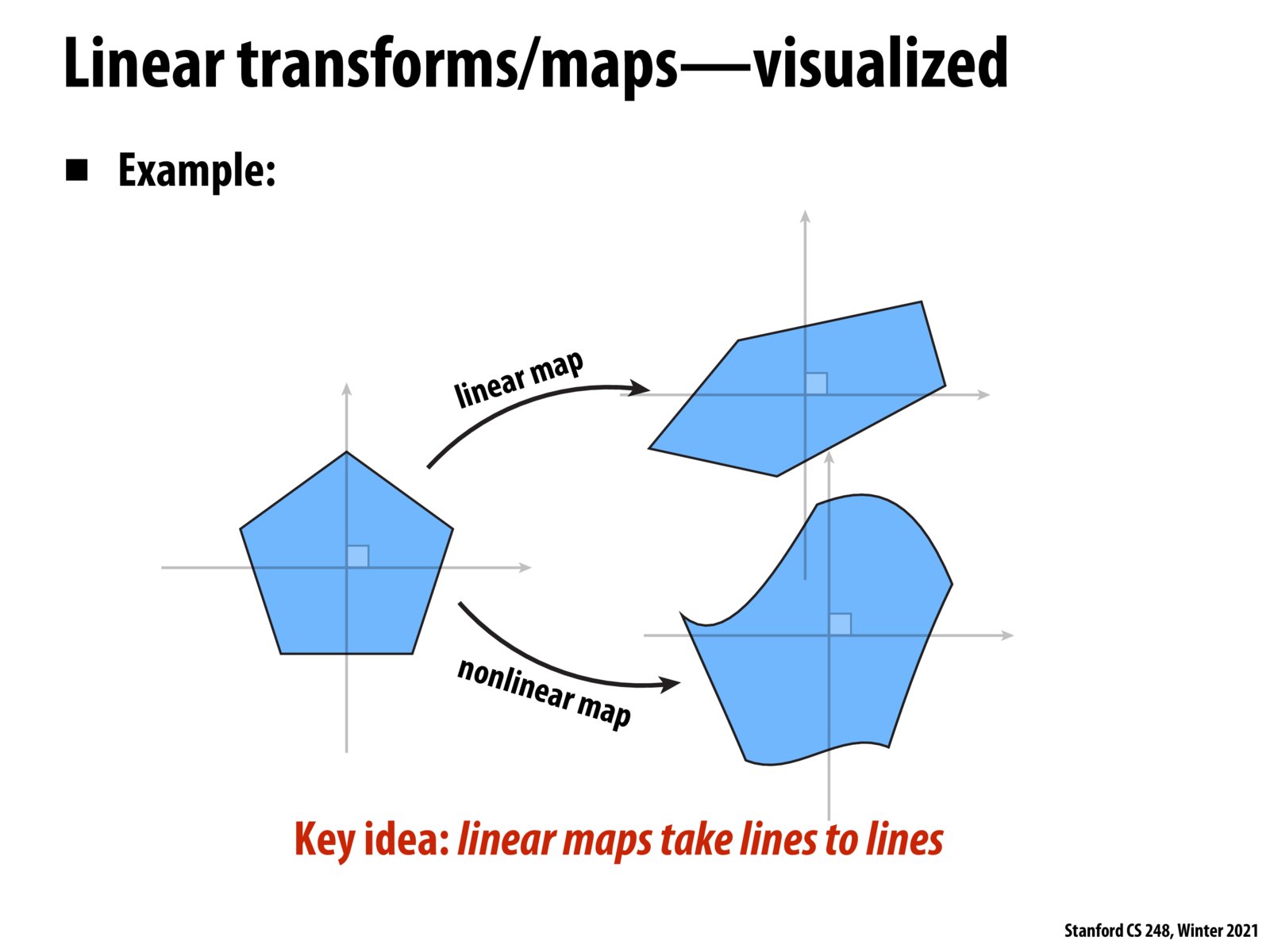
I guess if you have an image behind a lens (water drop, glass, etc), that's gonna to be transformed nonlinearly in general. Also creating a planar map from a spherical object (earth) and vice versa is nonlinear operation. Of course they follows some rule rather than random amorphous-ing :)

I actually think images behind lenses, especially artificially made ones, are generally transformed linearly, for example prescription glasses, camera lenses. But of course it depends on what we define as lens and the shape and curvatures of the lens. Water drops and drinking classes seem like good examples as their transformations seem a lot more complicated.

I think perhaps nonlinear maps had more relevance in the era of non-digitized screens (ie phosphorous screens like in scopes) that could draw "anywhere" in a continuous fashion. Today, our screens have such high pixel density that it seems like non linear mapping should never practically be used (since we can just represent the non linear maps as many small linear elements).