Warps are essentially separated and squashed down execution units! Each warp in this example holds 32 register sets for a specific thread. Because of this, thread blocks that are run in parallel are executed in the same fashion as SIMD instructions. If each thread in the 32-thread wide vector has the same instruction, we are able to run them as a SIMD vector. The masking properties are similar.

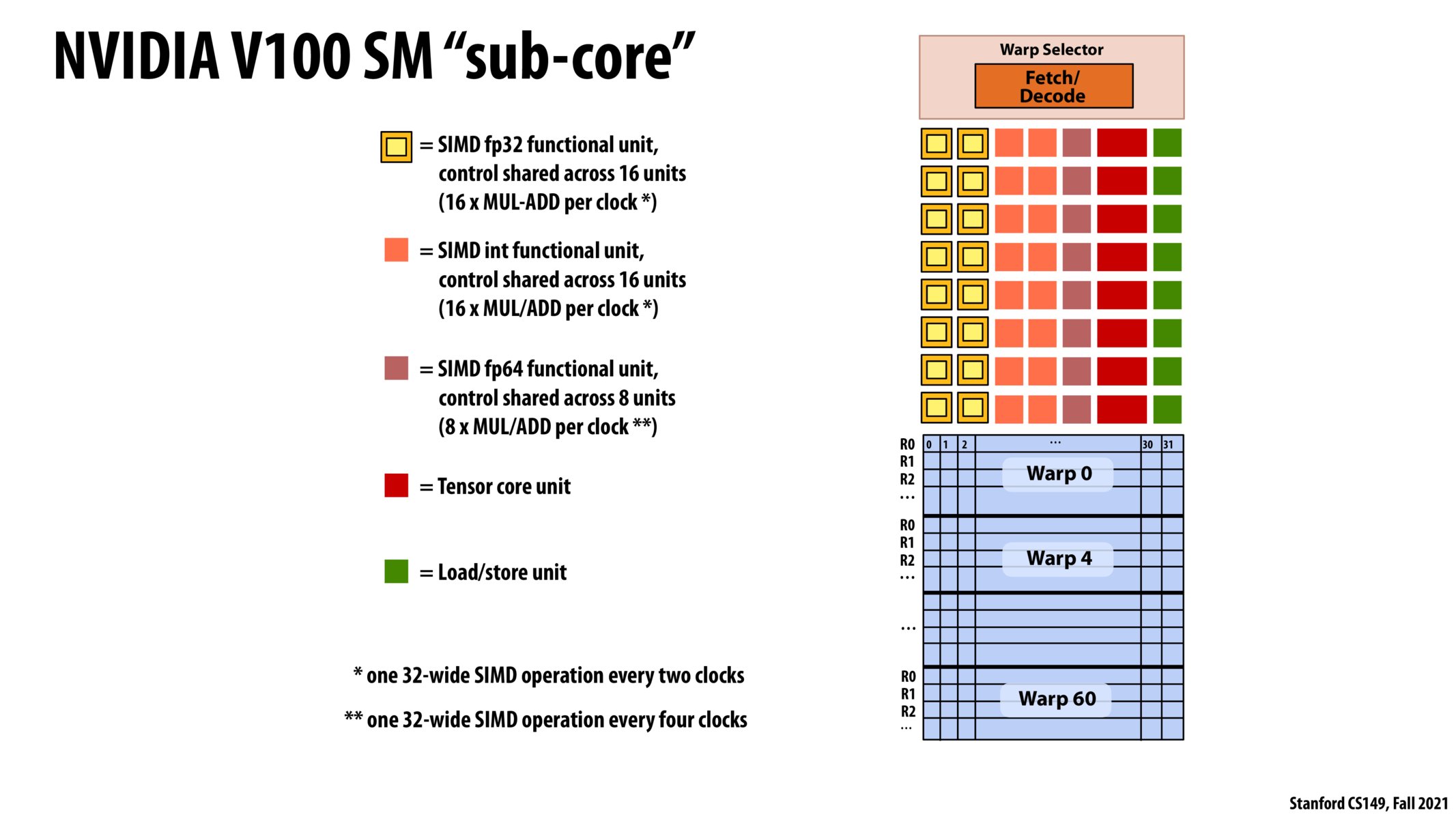
I am a little confused about why we choose this warp design over a pure SIMD implementation. Is it because warp also allows us to run scalar instructions at the cost of divergence (not using the vector ALUs)?

@leave I was wondering the same. My guess is that having warps gives you some more flexibility overall. For example, you could have divergent reads/writes and divergent control flow. And also you can have different sets of registers.

This link discusses SIMD vs SIMT (what nvidia calls this design)

https://yosefk.com/blog/simd-simt-smt-parallelism-in-nvidia-gpus.html

In summary, there are three things that you gain from SIMT 1. single instruction, multiple register sets. In other words, you are running the same instruction in many "threads" with different sets of registers. A side effect is you can write code that looks like scalar code, rather than using awful vector intrinsics keyboard mash function names. I suppose that it may be possible to write a compiler that somehow bypasses this and does a pure ALU approach. 2. single instruction, multiple addresses. You can load/write to divergent memory addresses, whereas it seemed that vector instructions had to load from contiguous memory. E.g. you could process an image column by column (not sure why you'd want to). I'm sure there are better real-world examples of this 3. single instruction, multiple program flow. This just opens the door to more options for parallelization and I think reduces the inefficiencies caused by masking on a pure vector ALU.

I'm curious to know how a tensor core unit is different from SIMD? aren't tensors just multi-dimensional sequences?