How do you determine what your homogenous coordinate is? I assume it's not always 1. What difference does it make?

I notice that the comments on slide 34, 35, and 36 are all asking the same question.

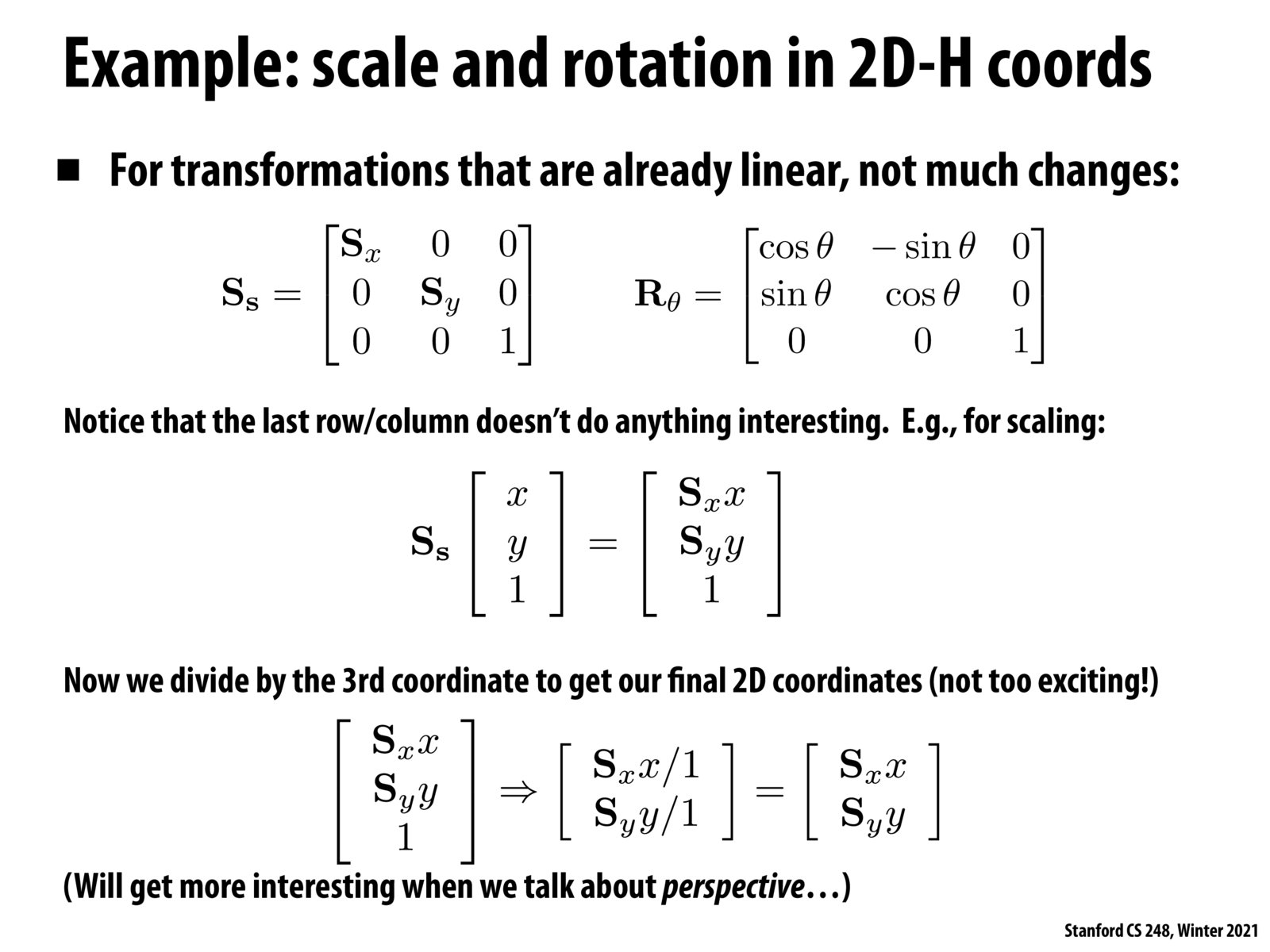
Homogeneous coordinates are a space where the mapping between homogeneous space and non-homogeneous space is performed by dividing all components by the extra component (which we typically denote as the "w" coordinate), and then dropping w. Here, since this is a 2D-homogeneous space, points in that space are represented by 3-vectors.

By this definition there are many points in 2D homogeneous space that correspond to the same point (x,y) in the 2D Euclidean space. For example (x,y,1), (2x, 2y, 2), (3x,3y,3), etc.

As a result, given a point (x,y) in 2D, constructing its homogeneous representation is given by constructing (wx, wy, w). (for any value of w).