I never considered until this point how the order in which tasks are assigned mattered but after seeing this image and the image on the next slide, It became completely clear. One question I have though is that how do you begin assigning the largest task first? It makes sense that we have to partition the workload into tasks but then do we have to perform some kind of sort on the task so the largest one shows up at the front of the work queue? For example, for the mandelbrot view1 the most computationally expensive tasks occurred in the middle of the image. How would we get the middle image tasks to appear at the beginning of the work queue?

I believe in the Mandelbrot homework problem we were manually assigning which rows of the image should be handled by each worker thread so it would not matter the order in which each thread executed each row. This order only plays a role if we were to use ISPC tasks for example which add each piece of work in a queue.

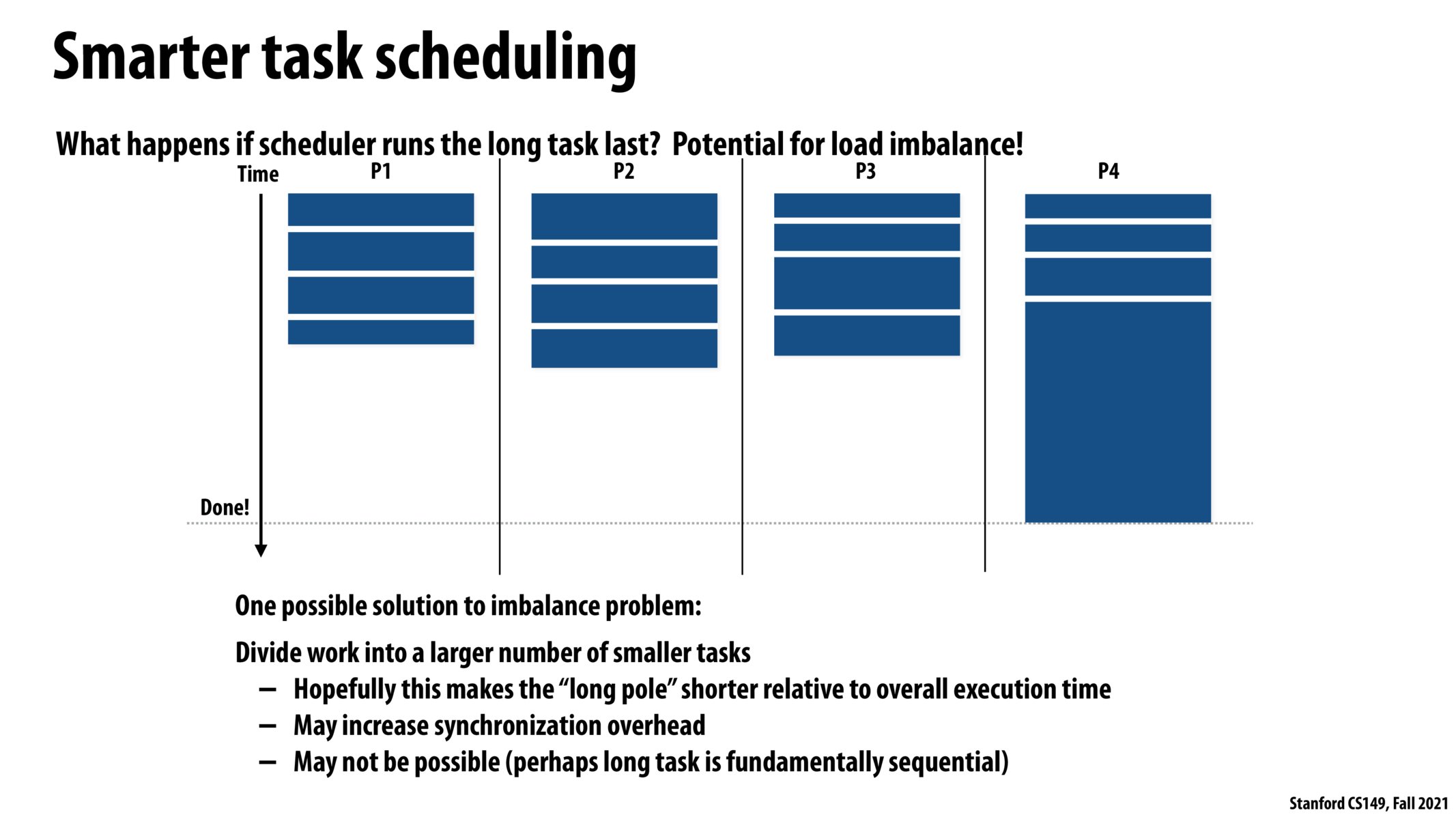
This slides raises an interesting point about the ordering of your work having major implications on the runtime of your program. This slide suggests splitting your tasks into as many smaller subtasks as possible to minimize the size of the "long pole" in comparison to the "short pole". I wonder if there are other heuristics that can be used to instead estimate how long a task will take, and then use this information to perform the scheduling.

This slide proposes a solution that fundamentally makes sense. But when assigning tasks, I don't think there is any way to concretely determine what will be the length of that task. If you can't say for sure how long a task will take, then I think this is really more of a theoretical solution.