This was somewhat covered in the review, but how can we be certain that n vectors in an n-dimensional space do in fact form a basis? Do they simply have to have a non-zero dot product?

I didn't know myself, so just going off wikipedia. There are two main conditions for n-vectors: 1. Be linearly independent, 2. Span n-dimensional space. If we concatenate these vectors to form a matrix, then we want this matrix to be of size n x n and have full rank (one way to check is determinant != 0). I think non-zero dot product won't work. Say we have two vectors (2, 2), (4, 4). They have a non-zero dot product: 24 + 24 = 16. But the vectors are linearly dependent.

• Looks like the message didn't format star for multiplication right: 24 + 24 = 16 should have been 2 x 4 + 2 x 4 = 16.

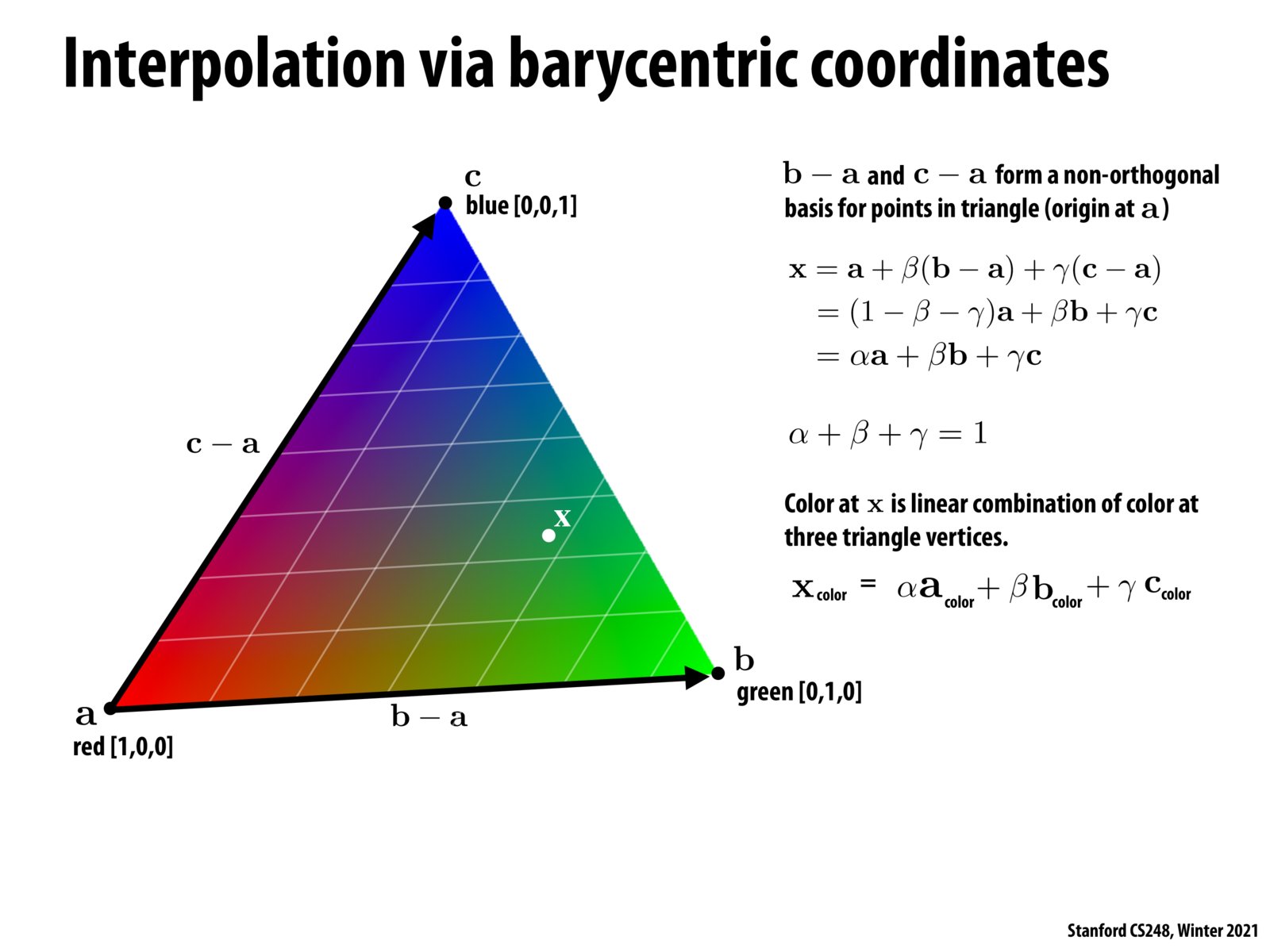
Are textures usually given by triangle?

Re:@jeyla, @alpaca -- a zero dot product sounds okay, because that corresponds to perpendicular directions (eg a right triangle). I believe "non-orthogonal" in this slide really means "not necessarily orthogonal".

Linear dependence also sounds fine; it would correspond to a triangle with one of the side lengths at zero but it doesn't seem like that breaks any of the equations here?