This slide is cool because it shows a way to geometrically visualize homogeneous coordinates. X and Y are the normal dimensions, but here we add a third dimension for W. Points X_1 and X in the plot represent the same point, just in two different coordinate spaces. You can convert X_1 from 2D-H to 2D space by scaling it down by w.

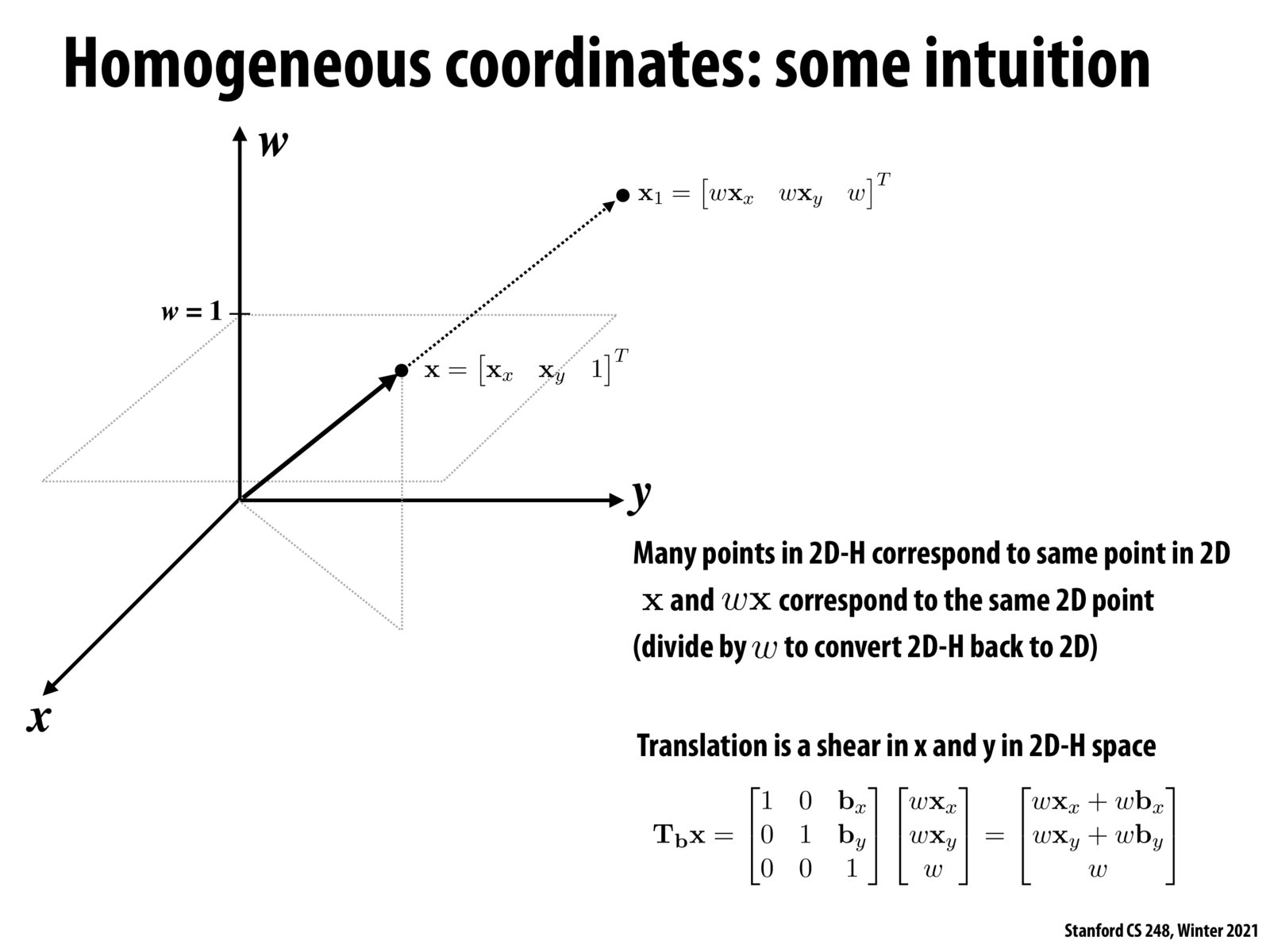
What does scaling by w do for us? Why would we ever convert to 2D-H coordinates with anything besides 1 in the third spot?

I have a same question as @jared711.

w can be used to encode the distance z coordinate of the object for the projection. The topic will be covered soon I think.

The w made a bit more sense for me in the next slide where it helps represent a square which allows for the shear. Unsure if there was a more practical use for it, though.

Maybe to some extent this is somewhat related to a 3D rendering space where you divide by the z coordinate - 2D is the same thing but everything is on the same z-plane.

A side note from the 231A class I'm taking right now, they also use this scaling factor w to help define point in infinity. This point in infinity is useful to represent the intersection of two parallel lines. So when w = 0, and when you divide by 0, essentially you are having a +inf coordinate for points. And interestingly, after perspective projection, this infinity can be projected into a finite number, and that also why two parallel lines have an intersection in perspective view. So my understanding is that, this extra dimension and w is used to help describe some behaviors that cannot be easily described in a normal way, such as non-linearity and infinity. http://web.stanford.edu/class/cs231a/course_notes/02-single-view-metrology.pdf

I have seen some situations that w = 0 means it a vector. w = 1 means it is a point.

^I've also seen this, particularly for things like velocities or computing deltas when two points are subtracted.

Has some nice + fairly intuitive properties: for example, it rotates but doesn't translate when a homogeneous transform is applied.